
Comet Halley’s position in May 2019. The view is from the north side of the solar system. Although the planets orbit our sun in a counterclockwise direction, Comet Halley orbits clockwise. Click here for Comet Halley’s present position, or change the date to view its position in any chosen year
Halley’s Comet, proud parent of two meteor showers, swings into the inner solar system about every 76 years. At such times, the sun’s heat causes the comet to loosen its icy grip over its mountain-sized conglomeration of ice, dust and gas. At each pass near the sun, the crumbly comet sheds a fresh trail of debris into its orbital stream. It lost about 1/1,000th of its mass during its last flyby in 1986. It’s because comets like Halley are so crumbly that we see annual meteor showers, like the Eta Aquariid meteor shower that’s going on now.
Keep reading to learn more about Comet Halley, the meteor showers it spawns, and about how astronomers calculate the velocities of meteors streaking across our sky.
Comet Halley on May 29, 1910 via Wikimedia Commons.
Kuiper Airborne Observatory acquired this image of Comet Halley in April 1986, as the comet crossed in front of the Milky Way. Image via NASA.
Comet Halley’s 2 meteor showers. Because Comet Halley has circled the sun innumerable times over countless millennia, cometary fragments litter its orbit. That’s why the comet doesn’t need to be anywhere near the Earth or the sun in order to produce a meteor shower. Instead, whenever our Earth in its orbit intersects Comet Halley’s orbit, cometary bits and pieces – oftentimes no larger than grains of sand or granules of gravel – smash into Earth’s upper atmosphere, to vaporize as fiery streaks across our sky: meteors.
It so happens we intersect Comet Halley’s orbit not once, but twice each year. In early May, we see bits of this comet as the annual Eta Aquariid meteor shower.
Then some six months later, in October, Earth in its orbit again intersects the orbital path of Comet Halley. This time around, these broken-up chunks from Halley’s Comet burn up in Earth’s atmosphere as the annual Orionid meteor shower.
By the way, these small fragments are called meteoroids when in outer space, and meteors when they vaporize in the Earth’s atmosphere.
Meteors in annual showers – made from the icy debris of comets – don’t hit the ground. They vaporize high in Earth’s atmosphere. The more rocky or metallic asteroids are what sometimes hit the ground, and then they are called meteorites.

Eta Aquariid meteors appear to radiate from near a famous asterism – or noticeable star pattern – called the Water Jar in Aquarius. The shower is coming up on the mornings of May 5 and 6, 2018.
Where is Comet Halley now? Often, astronomers like to give distances of solar system objects in terms of astronomical units (AU), which is the sun-Earth distance. Comet Halley lodges 0.587 AU from the sun at its closest point to the sun (perihelion) and 35.3 AU at its farthest point (aphelion).
In other words, Halley’s Comet resides about 60 times farther from the sun at its closest than it does at its farthest.
It was last at perihelion in 1986, and will again return to perihelion in 2061.
At present, Comet Halley lies outside the orbit of Neptune, and not far from its aphelion point. See the image at the top of this post – for May, 2017 – via Fourmilab.
Even so, meteroids swim throughout Comet Halley’s orbital stream, so each time Earth crosses the orbit of Halley’s Comet, in May and October, these meteoroids turn into incandescent meteors once they plunge into the Earth’s upper atmosphere.
Sideways view shows that the orbit of Halley’s Comet is highly inclined to the plane of the ecliptic. Green color depicts the part of orbit to the south of the ecliptic (Earth-sun orbital plane) while the blue highlights the part of the orbit to the north of the ecliptic.
Of course, Comet Halley isn’t the only comet that produces a major meteor shower …
Parent bodies of other major meteor showers
| Meteor Shower | Parent Body | Semi-major axis | Orbital Period | Perihelion | Aphelion |
| Quadrantids | 2003 EH1 (asteroid) | 3.12 AU | 5.52 years | 1.19 AU | 5.06 AU |
| Lyrids | Comet Thatcher | 55.68 AU | 415 years | 0.92 AU | 110 AU |
| Eta Aquariids | Comet 1/P Halley | 17.8 AU | 75.3 years | 0.59 AU | 35.3 AU |
| Delta Aquariids | Comet 96P/Machholz | 3.03 AU | 5.28 years | 0.12 AU | 5.94 AU |
| Perseids | Comet 109P/Swift-Tuttle | 26.09 AU | 133 years | 0.96 AU | 51.23 AU |
| Draconids | Comet 21P/Giacobini–Zinner | 3.52 AU | 6.62 years | 1.04 AU | 6.01 AU |
| Orionids | Comet 1/P Halley | 17.8 AU | 75.3 years | 0.59 AU | 35.3 AU |
| Taurids | Comet 2P/Encke | 2.22 AU | 3.30 years | 0.33 AU | 4.11 AU |
| Leonids | Comet 55P/Tempel-Tuttle | 10.33 AU | 33.22 years | 0.98 AU | 19.69 AU |
| Geminids | 3200 Phaethon (asteroid) | 1.27 AU | 1.43 years | 0.14 AU | 2.40 AU |
How fast do meteors from Comet Halley travel? If we can figure how fast Comet Halley travels at the Earth’s distance from the sun, we should also be able to figure out how fast these meteors fly in our sky.
Some of you may know that a solar system body, such as a planet or comet, goes faster in its orbit as it nears the sun and more slowly in its orbit as it gets farther away. Halley’s Comet swings inside the orbit of Venus at perihelion – the comet’s nearest point to the sun. At aphelion – its most distant point – Halley’s Comet goes all the way beyond the orbit of Neptune, the solar system’s outermost (known) planet.
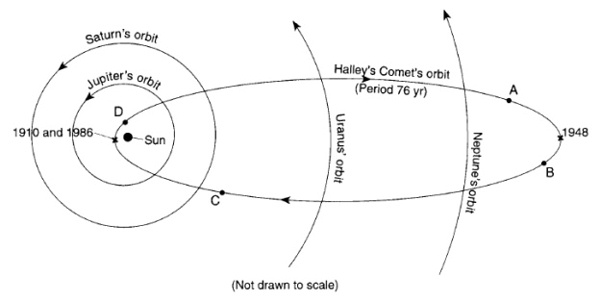
Diagram via SurveyMonkey. We’re looking down upon the north side of the solar system plane. The planets revolve around the sun counterclockwise, and Halley’s Comet revolves around the sun clockwise.
When the meteoroids from the orbital stream of Halley’s Comet streak across the sky as Eta Aquariid or Orionid meteors, we know these meteoroids/meteors have to be one astronomical unit (Earth’s distance) from the sun. It might be tempting to assume that these meteoroids at one astronomical unit from the sun travel through space at the same speed Earth does: 67,000 miles per hour (108,000 km/h).
However, the velocity of these meteoroids through space does not equal that of Earth at the Earth’s distance from the sun. For that to happen, Earth and Halley’s Comet would have to orbit the sun in the same period of time. But the orbital periods of Earth and Comet Halley are vastly different. Earth takes one year to orbit the sun whereas Halley’s Comet takes about 76 years.
However, thanks to the great genius, Isaac Newton, we can compute the velocity of these meteoroids/meteors at the Earth’s distance from the sun by using Newton’s Vis-viva equation, his poetic rendition of instantaneous motion.
The answer, giving the velocity of these meteoroids through space at the Earth’s distance from the sun, is virtually at our fingertips. All we need to know is Comet Halley’s semi-major axis (mean distance from the sun) in astronomical units. Here you have it:
Comet Halley’s semi-major axis = 17.8 astronomical units.

Once we know is a comet’s semi-major axis in astronomical units, we can compute its velocity at any distance from the sun with the easy-to-use Vis-viva equation. The sun resides at one of the two foci of the comet’s elliptical orbit.
In the easy-to-use Vis-viva equation below, r = distance from sun in astronomical units, and a = semi-major axis of Comet Halley’s orbit in astronomical units. In other words, r = 1 AU and a = 17.8 AU.
Vis-viva equation (r = distance from sun = 1 AU; and a = semi-major axis = 17.8 AU):
Velocity = 67,000 x the square root of (2/r – 1/a)
Velocity = 67,000 x the square root of (2/1 – 1/17.8)
Velocity = 67,000 x the square root of (2 – 0.056)
Velocity = 67,000 x the square root of 1.944
Velocity = 67,000 x 1.39
Velocity = 93,130 miles per hour or 25.87 miles per second
The above answer gives the velocity of these meteoroids through space at the Earth’s distance from the sun. However, if these meteoroids were to hit Earth’s atmosphere head-on, that would push the velocity up to an incredible 160,130 miles per hour (257,704 km/h) because 93,130 + 67,000 = 160,130. NASA gives the velocity for the Eta Aquariid meteors and Orionid meteors at 148,000 miles per hour (238,000 km/h), which suggests the collision of these meteoroids/meteors with Earth is not all that far from head-on.
We can also use the Vis-viva equation to find out the velocity of Halley’s Comet (or its meteoroids) at the perihelion distance of 0.59 AU and aphelion distance of 35.3 AU.
Perihelion velocity = 122,331 miles per hour (200,000 km/h)
Aphelion velocity = 1,464 miles per hour (2,400 km/h)
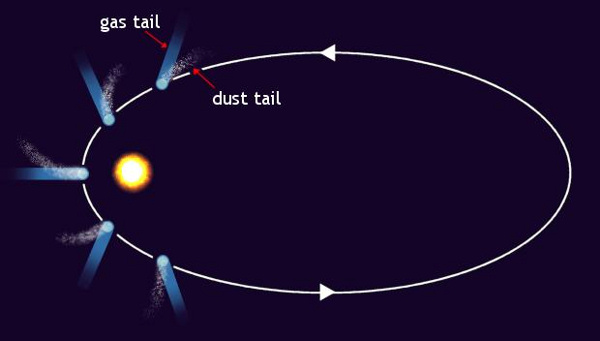
Comets develop gas and dust tails as they approach the sun. Depending on the comet, the comet can orbit the sun counter-clockwise (as above) or clockwise (as Comet Halley does). Read more: Why do comets develop tails?
Bottom line: The famous Comet Halley spawns the Eta Aquariids – going on now – and the Orionids in October. Plus where the comet is now, parent bodies of other meteor showers … and Isaac Newton’s Vis-viva equation, his poetic rendition of instantaneous motion.
from EarthSky http://bit.ly/2GV5VSr

Comet Halley’s position in May 2019. The view is from the north side of the solar system. Although the planets orbit our sun in a counterclockwise direction, Comet Halley orbits clockwise. Click here for Comet Halley’s present position, or change the date to view its position in any chosen year
Halley’s Comet, proud parent of two meteor showers, swings into the inner solar system about every 76 years. At such times, the sun’s heat causes the comet to loosen its icy grip over its mountain-sized conglomeration of ice, dust and gas. At each pass near the sun, the crumbly comet sheds a fresh trail of debris into its orbital stream. It lost about 1/1,000th of its mass during its last flyby in 1986. It’s because comets like Halley are so crumbly that we see annual meteor showers, like the Eta Aquariid meteor shower that’s going on now.
Keep reading to learn more about Comet Halley, the meteor showers it spawns, and about how astronomers calculate the velocities of meteors streaking across our sky.
Comet Halley on May 29, 1910 via Wikimedia Commons.
Kuiper Airborne Observatory acquired this image of Comet Halley in April 1986, as the comet crossed in front of the Milky Way. Image via NASA.
Comet Halley’s 2 meteor showers. Because Comet Halley has circled the sun innumerable times over countless millennia, cometary fragments litter its orbit. That’s why the comet doesn’t need to be anywhere near the Earth or the sun in order to produce a meteor shower. Instead, whenever our Earth in its orbit intersects Comet Halley’s orbit, cometary bits and pieces – oftentimes no larger than grains of sand or granules of gravel – smash into Earth’s upper atmosphere, to vaporize as fiery streaks across our sky: meteors.
It so happens we intersect Comet Halley’s orbit not once, but twice each year. In early May, we see bits of this comet as the annual Eta Aquariid meteor shower.
Then some six months later, in October, Earth in its orbit again intersects the orbital path of Comet Halley. This time around, these broken-up chunks from Halley’s Comet burn up in Earth’s atmosphere as the annual Orionid meteor shower.
By the way, these small fragments are called meteoroids when in outer space, and meteors when they vaporize in the Earth’s atmosphere.
Meteors in annual showers – made from the icy debris of comets – don’t hit the ground. They vaporize high in Earth’s atmosphere. The more rocky or metallic asteroids are what sometimes hit the ground, and then they are called meteorites.

Eta Aquariid meteors appear to radiate from near a famous asterism – or noticeable star pattern – called the Water Jar in Aquarius. The shower is coming up on the mornings of May 5 and 6, 2018.
Where is Comet Halley now? Often, astronomers like to give distances of solar system objects in terms of astronomical units (AU), which is the sun-Earth distance. Comet Halley lodges 0.587 AU from the sun at its closest point to the sun (perihelion) and 35.3 AU at its farthest point (aphelion).
In other words, Halley’s Comet resides about 60 times farther from the sun at its closest than it does at its farthest.
It was last at perihelion in 1986, and will again return to perihelion in 2061.
At present, Comet Halley lies outside the orbit of Neptune, and not far from its aphelion point. See the image at the top of this post – for May, 2017 – via Fourmilab.
Even so, meteroids swim throughout Comet Halley’s orbital stream, so each time Earth crosses the orbit of Halley’s Comet, in May and October, these meteoroids turn into incandescent meteors once they plunge into the Earth’s upper atmosphere.
Sideways view shows that the orbit of Halley’s Comet is highly inclined to the plane of the ecliptic. Green color depicts the part of orbit to the south of the ecliptic (Earth-sun orbital plane) while the blue highlights the part of the orbit to the north of the ecliptic.
Of course, Comet Halley isn’t the only comet that produces a major meteor shower …
Parent bodies of other major meteor showers
| Meteor Shower | Parent Body | Semi-major axis | Orbital Period | Perihelion | Aphelion |
| Quadrantids | 2003 EH1 (asteroid) | 3.12 AU | 5.52 years | 1.19 AU | 5.06 AU |
| Lyrids | Comet Thatcher | 55.68 AU | 415 years | 0.92 AU | 110 AU |
| Eta Aquariids | Comet 1/P Halley | 17.8 AU | 75.3 years | 0.59 AU | 35.3 AU |
| Delta Aquariids | Comet 96P/Machholz | 3.03 AU | 5.28 years | 0.12 AU | 5.94 AU |
| Perseids | Comet 109P/Swift-Tuttle | 26.09 AU | 133 years | 0.96 AU | 51.23 AU |
| Draconids | Comet 21P/Giacobini–Zinner | 3.52 AU | 6.62 years | 1.04 AU | 6.01 AU |
| Orionids | Comet 1/P Halley | 17.8 AU | 75.3 years | 0.59 AU | 35.3 AU |
| Taurids | Comet 2P/Encke | 2.22 AU | 3.30 years | 0.33 AU | 4.11 AU |
| Leonids | Comet 55P/Tempel-Tuttle | 10.33 AU | 33.22 years | 0.98 AU | 19.69 AU |
| Geminids | 3200 Phaethon (asteroid) | 1.27 AU | 1.43 years | 0.14 AU | 2.40 AU |
How fast do meteors from Comet Halley travel? If we can figure how fast Comet Halley travels at the Earth’s distance from the sun, we should also be able to figure out how fast these meteors fly in our sky.
Some of you may know that a solar system body, such as a planet or comet, goes faster in its orbit as it nears the sun and more slowly in its orbit as it gets farther away. Halley’s Comet swings inside the orbit of Venus at perihelion – the comet’s nearest point to the sun. At aphelion – its most distant point – Halley’s Comet goes all the way beyond the orbit of Neptune, the solar system’s outermost (known) planet.

Diagram via SurveyMonkey. We’re looking down upon the north side of the solar system plane. The planets revolve around the sun counterclockwise, and Halley’s Comet revolves around the sun clockwise.
When the meteoroids from the orbital stream of Halley’s Comet streak across the sky as Eta Aquariid or Orionid meteors, we know these meteoroids/meteors have to be one astronomical unit (Earth’s distance) from the sun. It might be tempting to assume that these meteoroids at one astronomical unit from the sun travel through space at the same speed Earth does: 67,000 miles per hour (108,000 km/h).
However, the velocity of these meteoroids through space does not equal that of Earth at the Earth’s distance from the sun. For that to happen, Earth and Halley’s Comet would have to orbit the sun in the same period of time. But the orbital periods of Earth and Comet Halley are vastly different. Earth takes one year to orbit the sun whereas Halley’s Comet takes about 76 years.
However, thanks to the great genius, Isaac Newton, we can compute the velocity of these meteoroids/meteors at the Earth’s distance from the sun by using Newton’s Vis-viva equation, his poetic rendition of instantaneous motion.
The answer, giving the velocity of these meteoroids through space at the Earth’s distance from the sun, is virtually at our fingertips. All we need to know is Comet Halley’s semi-major axis (mean distance from the sun) in astronomical units. Here you have it:
Comet Halley’s semi-major axis = 17.8 astronomical units.

Once we know is a comet’s semi-major axis in astronomical units, we can compute its velocity at any distance from the sun with the easy-to-use Vis-viva equation. The sun resides at one of the two foci of the comet’s elliptical orbit.
In the easy-to-use Vis-viva equation below, r = distance from sun in astronomical units, and a = semi-major axis of Comet Halley’s orbit in astronomical units. In other words, r = 1 AU and a = 17.8 AU.
Vis-viva equation (r = distance from sun = 1 AU; and a = semi-major axis = 17.8 AU):
Velocity = 67,000 x the square root of (2/r – 1/a)
Velocity = 67,000 x the square root of (2/1 – 1/17.8)
Velocity = 67,000 x the square root of (2 – 0.056)
Velocity = 67,000 x the square root of 1.944
Velocity = 67,000 x 1.39
Velocity = 93,130 miles per hour or 25.87 miles per second
The above answer gives the velocity of these meteoroids through space at the Earth’s distance from the sun. However, if these meteoroids were to hit Earth’s atmosphere head-on, that would push the velocity up to an incredible 160,130 miles per hour (257,704 km/h) because 93,130 + 67,000 = 160,130. NASA gives the velocity for the Eta Aquariid meteors and Orionid meteors at 148,000 miles per hour (238,000 km/h), which suggests the collision of these meteoroids/meteors with Earth is not all that far from head-on.
We can also use the Vis-viva equation to find out the velocity of Halley’s Comet (or its meteoroids) at the perihelion distance of 0.59 AU and aphelion distance of 35.3 AU.
Perihelion velocity = 122,331 miles per hour (200,000 km/h)
Aphelion velocity = 1,464 miles per hour (2,400 km/h)

Comets develop gas and dust tails as they approach the sun. Depending on the comet, the comet can orbit the sun counter-clockwise (as above) or clockwise (as Comet Halley does). Read more: Why do comets develop tails?
Bottom line: The famous Comet Halley spawns the Eta Aquariids – going on now – and the Orionids in October. Plus where the comet is now, parent bodies of other meteor showers … and Isaac Newton’s Vis-viva equation, his poetic rendition of instantaneous motion.
from EarthSky http://bit.ly/2GV5VSr

Aucun commentaire:
Enregistrer un commentaire